텐서플로 정리 1탄

텐서플로공부

텐서플로 정리 1탄

백준파이썬개발자:프로젝트골드 2024. 1. 11. 00:52

위코드는 코랩에서 진행하므로 별도의 설치가 필요하지 않습니다.

구글에 코랩이라고 검색하면 무료로 사용할 수 있는 파이썬 환경입니다.

# 3.6 텐서플로우 불러오기, 버전 확인 에러

import tensorflow as tf

print(tf.__version__)

위코드를 통해서 텐서플로의 버전을 확인한다.

import tensorflow는 tensorflow를 가져온다는 의미이다.

as는 이것은 tf로 이름을 바꾸어 명명한다는 의미이다.

일반적으로 tensorflow라고 전부 적으면 귀찮지않은가 그래서 tf로 명명한다.

tf.__version__은 텐서플로의 버전을 확인한다.

2024년 1월 10일 기준으로

2.15.0이라는 결과가 나왔다.

균일분포 vs 정규분포

이제 uniform이라는 함수를 정리 하겠다.

tf.random.uniform([1],0,1)

위함수의 random.uniform([배열의크기],최저숫자,최대숫자)은 랜덤한 숫자를 만들어주는 것이다.

배열의 크기와 숫자의 범위를 지정하여 만들어준다.

아래의 경우 배열의 크기는 1이몀 0부터 1까지의 숫자사이값을 가져오는 코드이다.

이제 normal이라는 코드를 소개하겠다.

# 3.9 랜덤한 수 여러 개 얻기 (정규 분포)

rand = tf.random.normal([4],0,1)

위함수의 random.uniform([배열의크기],평균,분산)은 랜덤한 숫자를 만들어주는 것이다.

배열의 크기와 숫자의 범위를 지정하여 만들어준다.

아래의 경우 배열의 크기는 1이며 평균은 0 분산이 1인 숫자를 만들어주는 코드이다.

위 균일분포와 정규분포차이를 정리하자면

균일분포는 지정한 범위안에 동일한확률로 값이 분포된다.

하지만 정규분포의 경우는 평균을 기점으로 값이 멀어져갈수록 분포가 줄어든다.

이때 분산이라는 값을 조정하여 얼마나 값이 멀어질지를 정하는 것이다.

# 3.10 sigmoid 함수

import math

def sigmoid(x):

return 1 / (1 + math.exp(-x))

위코드의 실제 수식은 아래와같다.

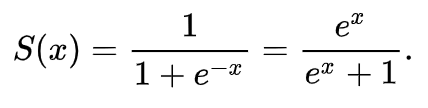
위 수식의 그래프는 다음과 같다.

이제 자세히 설명하겠다.

시그모이드를 사용하는 이유는 인공지능에게 입력하는 값이 0부터 1사이값이 들어가면 이상적일 것이다.

값의 편차가 적기 때문이다.

하지만 실제로는 절대값이 큰수를 넣어야하는 경우도 생긴다.

시그모이드는 값이 크면 클수록 가중치를 더해주고 작을수록 0에 가까워 이상적인 결과를 이끌어낸다.

이제 인공지능에게 학습을 시작해보자

# 3.11 뉴런의 입력과 출력 정의

x = 1

y = 0

w = tf.random.normal([1],0,1)

output = sigmoid(x * w)

print(output)

위코드를 통해서 학습하면 된다.

x값은 학습시킬 값이며

y값은 학습결과이다.

w값은 normal이기에 정규분포를 사용한것을 알수 있다.

가중치로 w값과 x값을 곱한후 시그모이드함수를 거쳐서 나온겂이 output에 저장된다.

본인이게는 0.6703849683852051라는 값이 나왔지만 사람마다 다를게 나올것이다.

그이유는 가중치는 랜덤한 숫자로 나오기때문이다.

경사하강법

# 3.12 경사 하강법을 이용한 뉴런의 학습

for i in range(1000):

output = sigmoid(x * w)

error = y - output

w = w + x * 0.1 * error

if i % 100 == 99:

print(i, error, output)

위코드를 통해서 진행힌다.

위에서 output를 계산하는 과정을 보여주었다.

이것을 y값에 근접하게 계산하는 방법은 output값과 y값차이를 구한다

이후 차이만큼 가중치값인 w를 바꾸어나간다.

이렇게 처음에는 랜덤한 숫자로 시작했지만 가중치w값이 y값과 점점 가까워지도록 하는 기법이다.

그래프로보면 다음과같다.

그림과같이 같이 손실함수를 최소한으로 만들어가면서 학습하는 기법으로 error라는 값이 적어지는 방향으로 학습하는 것이다.그러던중 어느순간부터 과적합이라고해서 학습을 하더라도 정확도가 오르지않고 떨어지는 구간이 생긴다.

그렇기에 다음과 같은 그래프가 완성이 된다.

과적합에대해서는 다음에 설명하겠다.

코드의 결과는 다음과같다.

99 -0.11460162599527696 0.11460162599527696 199 -0.05563294145964074 0.05563294145964074 299 -0.036298813153364765 0.036298813153364765 399 -0.026843702145993898 0.026843702145993898 499 -0.021264985787206467 0.021264985787206467 599 -0.01759269127853435 0.01759269127853435 699 -0.014995367085711144 0.014995367085711144 799 -0.013062655422457168 0.013062655422457168 899 -0.011569087945317616 0.011569087945317616 999 -0.010380669763186313 0.010380669763186313

x가 0일때의 학습

# 3.13 x=0 일 때 y=1 을 얻는 뉴런의 학습

x = 0

y = 1

w = tf.random.normal([1],0,1)

for i in range(1000):

output = sigmoid(x * w)

error = y - output

w = w + x * 0.1 * error

if i % 100 == 99:

print(i, error, output)

위값의 결과가 어떻게 되었을것같은가

정답은 학습이 이루어지지 않았다.

결과는 다음과같다.

왜 이런결과가 나왔을까?

간단하다 x값이 0인데 아무리 값을 곱하더라도 0이기 때문이다.

그렇기때문에 가중치인 w값을 아무리 바꾸더라도 값이 변하지 않기때문이다.

그것을 해결하는 방법은 바이어스라고 불리는 편향을 넣는 것이다.

아래코드를 보자

학습편향

# 3.14 x=0 일 때 y=1 을 얻는 뉴런의 학습에 편향을 더함

x = 0

y = 1

w = tf.random.normal([1],0,1)

b = tf.random.normal([1],0,1)

for i in range(1000):

output = sigmoid(x * w + 1 * b)

error = y - output

w = w + x * 0.1 * error

b = b + 1 * 0.1 * error

if i % 100 == 99:

print(i, error, output)

달라진점은 b라는변수를추가했다.

그동안 w라는 가중치값만 변화시켰다.

하지만 이번에는 b라는 변수로 편향을 추가하였다.

수식으로 따지면 w*x -> w*x+b 이런 수식으로 바뀐것이다.

결과는 다음과같다.

점점 에러가 줄어들고 값이 1에 가까워진다.

and게이트 학습

# 3.16 첫번째 신경망 네트워크 : AND

import numpy as np

x = np.array([[1,1], [1,0], [0,1], [0,0]])

y = np.array([[1], [0], [0], [0]])

w = tf.random.normal([2],0,1)

b = tf.random.normal([1],0,1)

b_x = 1

for i in range(2000):

error_sum = 0

for j in range(4):

output = sigmoid(np.sum(x[j]*w)+b_x*b)

error = y[j][0] - output

w = w + x[j] * 0.1 * error

b = b + b_x * 0.1 * error

error_sum += error

if i % 200 == 199:

print(i, error_sum)

위코드는 and게이트를 학습하는 것이다.

and게이트가 모르는 사람을 위해서 설명하자면

들어오는 두수의 값이 1이라면 1이고 나머지 경우는 0이다.

위 코드를 보면 1,1일경우는 1이지만 1,0일경우는 0이다. 0,0이면 당연히 0으로 출력되는 것이다.

이것을 경사하강법을 통해서 학습을 진행해보겠습니다.

이번에 수식은 np.sum(x[j]*w)+b_x*b이다.

의문점이 생길것이다.

1,1과같이 배열의 크기가 2인데 출력값이 1로 통일을 해야한다는 점이다.

이문제를 배열의 합을 구하는 것으로 문제를 해결하였다.

간단하다. 1,1일경우 값을 2라고 보고 계산을하겠다는것이다.

1,0이면 1로 계산하고 0,0,이라면 0으로 계산한다.

그렇게 이전과같은방식으로 경사하강법을 사용하면 아래와 같은 결과가 나온다.

이제 결과를 정리해보자

# 3.20 AND 네트워크의 평가

for i in range(4):

print('X:', x[i], 'Y:', y[i], 'Output:', sigmoid(np.sum(x[i]*w)+b))

이코드를 통해서 각자입력에 대한결과를 출력한다.

1,1 그리고 1,0 또 0,1은 결과가 정상적이다.

0,0의 경우는 왜값이 2가 나왔지라는 착각을 할 수있다.

2가 아니다 뒤에 e라는 표현이 보이는가

e-05라는 표현으로 1/10^5를 곱하라는 의미이다.

즉 0.0000232~로 되어있는 숫자이다.

and게이트는 학습이 잘되었다는 증거다.

# 3.21 두번째 신경망 네트워크 : OR

import numpy as np

x = np.array([[1,1], [1,0], [0,1], [0,0]])

y = np.array([[1], [1], [1], [0]])

w = tf.random.normal([2],0,1)

b = tf.random.normal([1],0,1)

b_x = 1

for i in range(2000):

error_sum = 0

for j in range(4):

output = sigmoid(np.sum(x[j]*w)+b_x*b)

error = y[j][0] - output

w = w + x[j] * 0.1 * error

b = b + b_x * 0.1 * error

error_sum += error

if i % 200 == 199:

print(i, error_sum)

위코드는 or게이트이다.

or게이트는 값이 값이 둘중하나라도 1이라면 1을 출력하는 게이트이다.

즉 1,1 또 1,0 그리고 0,1은 1이라는 값을 낸다.

하지만 0,0의 경우는0 이라는 값을 낸다.

결과는 정상적으로 작동하기해 해보기를 권장한다.

결과를 확인하는 코드는 다음과같다.

# 3.22 OR 네트워크의 평가

for i in range(4):

print('X:', x[i], 'Y:', y[i], 'Output:', sigmoid(np.sum(x[i]*w)+b))

XOR 학습

# 3.23 세번째 신경망 네트워크 : XOR

import numpy as np

x = np.array([[1,1], [1,0], [0,1], [0,0]])

y = np.array([[0], [1], [1], [0]])

w = tf.random.normal([2],0,1)

b = tf.random.normal([1],0,1)

b_x = 1

for i in range(2000):

error_sum = 0

for j in range(4):

output = sigmoid(np.sum(x[j]*w)+b_x*b)

error = y[j][0] - output

w = w + x[j] * 0.1 * error

b = b + b_x * 0.1 * error

error_sum += error

if i % 200 == 199:

print(i, error_sum)

위코드는 xor 게이트를 학습시키는 코드이다.

xor게이트는 값이 다를 경우에는 1을 출력하고 같은경우 0을 출력하는 코드이다.

예를들어 1,1와 0,0인경우는 0을 출력한다 하지만 1,0과 0,1인경우는 1을 출력하는 게이트이다.

결과를 학인해보자

# 3.24 XOR 네트워크의 평가

for i in range(4):

print('X:', x[i], 'Y:', y[i], 'Output:', sigmoid(np.sum(x[i]*w)+b))

다음과같이 값이 이상하다.

값이 0.5라는 값에 수렴한다.

이것인 인공지능이 쇠퇴기를 맞았던이유이다.

xor도 학습시키지 못하는 인공지능이기였기에 때문이다.

이것의 해결방법음 다음과같다.

신경망을 이용한 학습

기존에는 가중치와 바이어스를 한번만 바꾸며 학습을 하였다.

즉 하나의 뉴런만을 사용했다는 의미이다.

하지만 이번학습에서는 3개의 뉴런을 사용한다.

아래코드는 2개의 뉴런을 통해서 입력을 받는다.

이후 2개의 뉴런을 통해서 얻은 값을 마지막 뉴런에 입력을 한다.

인공지능이 학습하여 결과를 도출한다.

아래코드를 해석해주겠다.

# 3.27 tf.keras 를 이용한 XOR 네트워크 계산

import numpy as np

x = np.array([[1,1], [1,0], [0,1], [0,0]])

y = np.array([[0], [1], [1], [0]])

model = tf.keras.Sequential([

tf.keras.layers.Dense(units=2, activation='sigmoid', input_shape=(2,)),

tf.keras.layers.Dense(units=1, activation='sigmoid')

])

model.compile(optimizer=tf.keras.optimizers.SGD(lr=0.3), loss='mse')

model.summary()

model부분은 이해가 될것이다. 2개의 뉴런으로 학습한후 마지막뉴런에 값을 전해서 예측을 진행하는 것이라고

complie의 SGD는 경사하강법을 사용하겠다는 의미이다.

lr=0.3은 학습율을 0.3으로 설정한것이다.

학습율이란 무엇일까? w의 앞에 0.1이라는 숫자가 있었을것이다.

이것이 오차를 계산후 한번에 많은 양을 학습하면 정확도가 떨어지기에 학습율을 적절히 조절해야한다.

그렇기에 이전에는 차이의 0.1만큼 곱하여 더했지만 이번엔 0.3을 곱한후 더하는 방식을 사용하는 것이다.

mse는 평균 제곱 오차를 이용하여 오차를 계산하는 방식을 채택한다는 의미이다.

model.summary의 결과는 다음과같다.

위값을 계산하는 방법은 간단하다.

입력한 차원수*유닛수 +유닛수이다.

계산을 하자면 2*2+2 =6이다.

1,0과같이 차원이 2개이므로 차원수는 2이고

유닛수는 2개로 설정하였다.

위식이 나오는 이유는 w와 b때문이다.

w로인해서 차원수*유닛수가 나오고

뒤이 +2를 하는 이유는 b때문이다.

아래 dense_3도 같은 방식으로 계산하면

2*1+1이다.

입력하는 차원수는 2개이다.

그이유는 이전에 유닛이 2개였기에 두개의 유닛으로 부터 학습한다.

케라스를 통한 XOR학습

# 3.28 tf.keras 를 이용한 XOR 네트워크 학습

history = model.fit(x, y, epochs=2000, batch_size=1)

여기서 epochs는 2000이라고 되어있는데 천번 학습을 한다는 의미이다.

batch_size는 한번에 많은 양을 학습하기에 버겁기때문에 나누어서 학습하겠다는 의미이다.

지금은 한번에 하나씩입력을 하겠다는 의미입니다.

학습결과는 다음과같다.

# 3.29 tf.keras 를 이용한 XOR 네트워크 평가

model.predict(x)

다음과같이 정상적으로 잘 학습한것을 알수 있다.

학습편향확인하기

# 3.30 XOR 네트워크의 가중치와 편향 확인

for weight in model.weights:

print(weight)

이코드는 각자 따로 돌려보기 바람